În analiza matematică, integrala unei funcții este o generalizare a noțiunilor de arie, masă, volum și sumă. Procesul de determinare a unei integrale se numește integrare. Spre deosebire de noțiunea înrudită de derivată, există mai multe definiții posibile ale integralei, fiecare cu suportul său tehnic. Acestea sunt însă compatibile. Oricare două moduri de integrare a unei funcții vor da aceleași rezultate când ambele sunt definite.
În mod intuitiv, integrala unei funcții continue, pozitive, f, de variabilă reală și luând valori reale, între două puncte a și b, reprezintă valoarea ariei mărginite de segmentele x=a, x=b, axa x și graficul funcției f. Formal, considerând
atunci integrala funcției f între a și b este măsura lui S.
Termenul "integrală" se poate referi și la noțiunea de primitivă a unei funcții, adică o funcție F a cărei derivată este funcția dată f. În acest caz, se numește integrală nedefinită, pe când integralele discutate în acest articol sunt numite integrale definite.
Principiile integrării au fost enunțate de Isaac Newton și Gottfried Wilhelm Leibniz la sfârșitul secolului al XVII-lea. Prin teorema fundamentală a calculului integral, pe care au dezvoltat-o independent unul de altul, integrarea este legată de derivare, iar integrala definită a unei funcții poate fi ușor calculată odată ce este cunoscută o primitivă a ei. Integralele și derivatele au devenit uneltele de bază ale analizei matematice, cu numeroase aplicații în știință și inginerie.
O definiție riguroasă a integralei a fost dată de Bernhard Riemann. Ea este bazata pe o trecere la limită prin care se aproximează aria unei regiuni curbilinii prin descompunerea acesteia în zone verticale subțiri. Din secolul al XIX-lea, au înceut să apară tipuri de integrale mai sofisticate, în care atât tipul funcției cât și domeniul peste care se face integrarea au început să fie generalizate. O integrală curbilinie este definită pentru funcții de două sau trei variabile, iar intervalul de integrare ![[a , b ]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
este înlocuit de o anumită curbă care leagă două puncte din plan sau din spațiu. Într-o integrală de suprafață, curba este înlocuită de o bucată de suprafață din spațiul tridimensional.
este înlocuit de o anumită curbă care leagă două puncte din plan sau din spațiu. Într-o integrală de suprafață, curba este înlocuită de o bucată de suprafață din spațiul tridimensional.
Integralele formelor diferențiale joacă un rol fundamental în geometria diferențială modernă. Aceste generalizări ale integralelor au apărut datorită necesităților din fizică, și joacă un rol important în formularea multor legi din fizică, în principal a celor din electrodinamică. Conceptele moderne ale integrării se bazează pe teoria matematică abstractă numităintegrală Lebesgue, dezvoltată de Henri Lebesgue.
Leibniz a introdus notația standard a integralei, de forma unui S alungit. Integrala din paragraful anterior se notează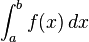 
. Semnul ∫ notează integrarea, a și b sunt extremitățile intervalului, f(x) este funcția care se integrează, iar dx notează variabila în care se face integrarea. La început, dx reprezenta o "cantitate infinitezimală", iar S-ul alungit însemna "sumă". Însă teoria modernă a integralei este construită pe alte fundamente, iar aceste simboluri tradiționale au devenit simple notații.
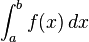. Semnul ∫ notează integrarea, a și b sunt extremitățile intervalului, f(x) este funcția care se integrează, iar dx notează variabila în care se face integrarea. La început, dx reprezenta o "cantitate infinitezimală", iar S-ul alungit însemna "sumă". Însă teoria modernă a integralei este construită pe alte fundamente, iar aceste simboluri tradiționale au devenit simple notații.